Impact of undefined behavior on performance.

Or when undefined behavior is our friend.

Undefined behavior has a bad reputation and as such is something that we are taught to avoid.

It takes a tremendous amount of work to define language behavior for every single possible case, so few if any programming language designers attempt doing so. But even though it’s generally nice when programs behave the way we expect them to, defining every aspect of program execution severely limits the number of optimizations that software and hardware is able to perform. That’s why even such important optimizations like tail-call elimination is mentioned only in Scheme specification.

But does it really matter in practice? Surely it’s just a topic for academic discussions and unlikely affect our apps, right? Well, let’s take a look at a simple function responsible for summing up the first n natural numbers and for reasons that will be mentioned below we’ll make the function generic and instantiate it with unsigned integer

	template<class T>
	T sum_of_n (T n) {
	T total = 0;
	for (T i = 1; i <= n; ++i) total += i;
	return total;
	}
	template unsigned int sum_of_n<unsigned int>(unsigned int n);

view raw sum_of_n.cpp hosted with ❤ by GitHub

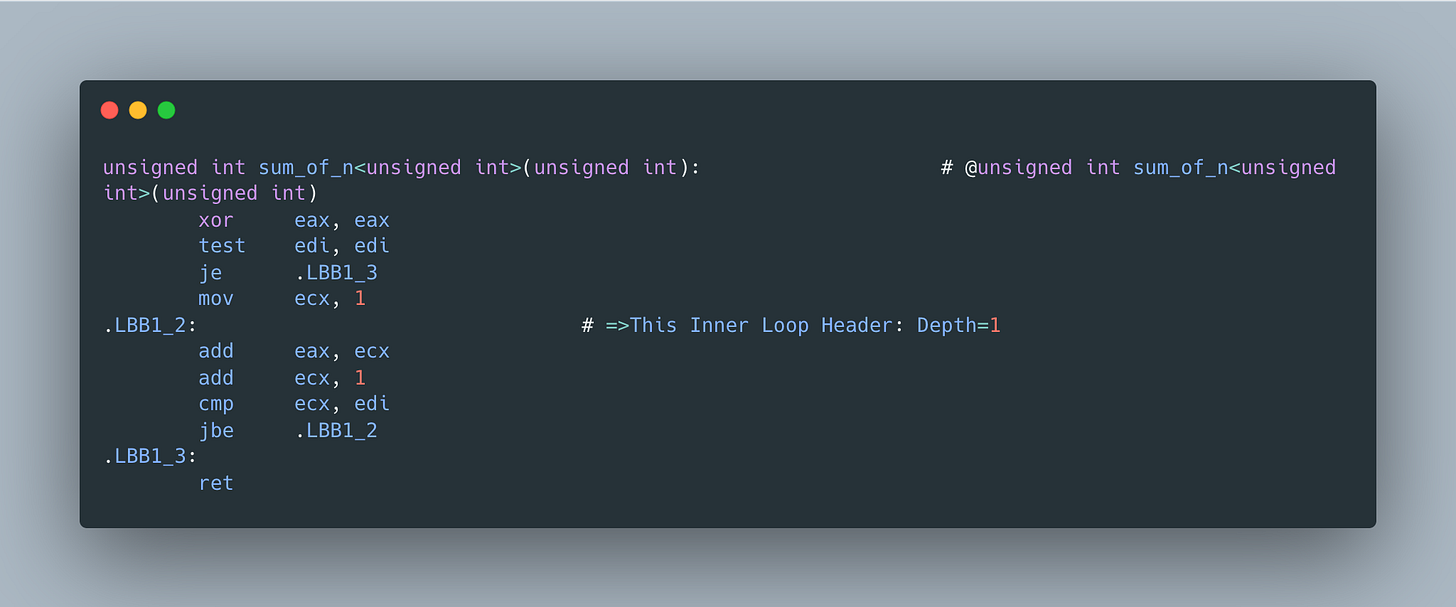
Its assembly follows closely its C++ version

where n=edi, total=eax and i=ecx. Even though it certainly does the job, at school we’ve learnt a much faster way to compute a sum of n natural numbers

so it’s a bit unfortunate that LLVM didn’t use this formula. But before giving up on compilers and starting implementing all optimizations by hand, let’s instantiate a signed integer version of the sum_of_n function using

template int sum_of_n<int>(int n);

and look at its assembly

It looks nothing like the assembly for the unsigned integer version and most importantly has no loops. Since it may not be obvious what compiler is doing here, the snippet below will hopefully make things easier to understand

rdi=n

eax=n-1

ecx=n-2

rcx=rcx*rax=(n-1)*(n-2)

rcx=rcx >> 1=(n-1)*(n-2)/2

eax=rcx+2*rdi=(n-1)*(n-2)/2+2*n=((n-1)*(n-2)+4*n)/2=(n^2-2*n-n+2+4*n)/2=(n^2+n+2)/2

eax=eax-1=(n^2+n+2-2)/2=n(n+1)/2

So turns out LLVM spotted the pattern and was able to replace a naive summation loop with the constant time formula! But why wouldn’t it do the same for unsigned integer version? The answer goes back to undefined behavior. Specifically unsigned integer overflow is well defined by both the C and C++ standards. The C99 standard (§6.2.5/9) states

A computation involving unsigned operands can never overflow, because a result that cannot be represented by the resulting unsigned integer type is reduced modulo the number that is one greater than the largest value that can be represented by the resulting type.

At the same time both standards state that signed integer overflow is undefined behavior (C99 standard (§3.4.3/1)):

An example of undefined behavior is the behavior on integer overflow

So undefined behavior is the reason why compilers like LLVM have more freedom when it comes to optimizations since they are not constrained by the overflow rules.

And how much impact does it have on runtime performance? Well even computing a sum for a relative small number 1000, according to cppbench, the signed version is 430X faster.

Interestingly, some developers criticize C++ for having these cases of undefined behavior and use this as an argument for using Rust, that has fewer cases of undefined behavior. So it’s interesting to check what Rust compiler does in these cases using functions below

	#[no_mangle]
	pub fn sum_of_n_unsigned(n: usize) -> usize {
	let mut total = 0;
	for i in 1..=n {
	total += i;
	}
	total
	}
	#[no_mangle]
	pub fn sum_of_n_signed(n: i32) -> i32 {
	let mut total = 0;
	for i in 1..=n {
	total += i;
	}
	total
	}

view raw sum_of_n.rs hosted with ❤ by GitHub

And unfortunately both versions use loops, similar to unsigned integer version in C++:

The reason for this is simple and stated in The Rustonomicon:

No matter what, Safe Rust can't cause Undefined Behavior.

As such it’s important to understand which behaviors are not defined in our programming languages and associated consequences.

You can play with the C++ version of code using Compiler explorer.