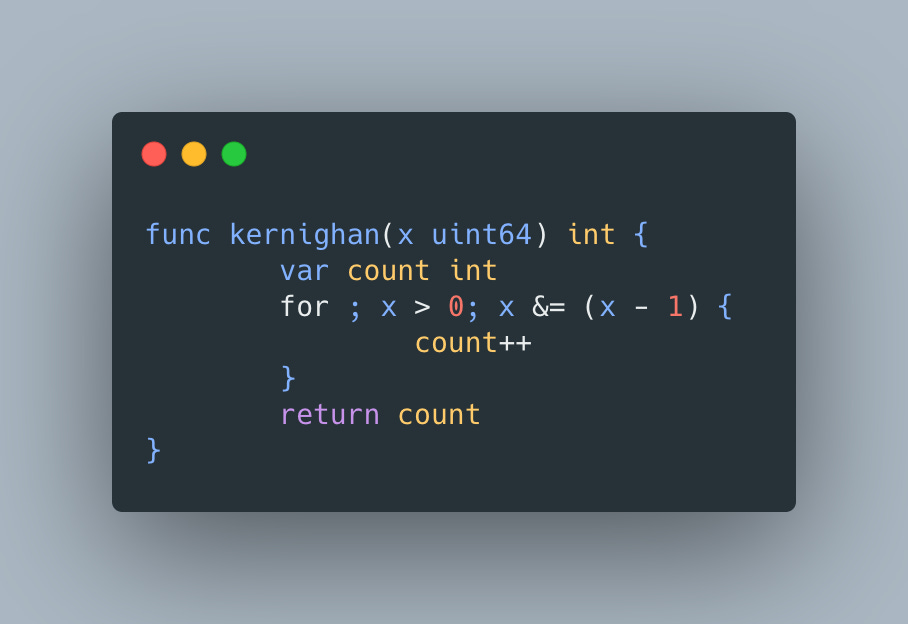
Counting the number of bits set in the integer, also known as population count, comes up fairly frequently in competitive programming and has a number of different implementations. In his “The C Programming Language 2nd Ed” book Kernighan has included a method based on unsetting rightmost bit until we get to 0:
Since the number of iterations is determined by the number of set bits, the complexity of this algorithm is O(number of set bits in n).
"Hacker's Delight", Chap. 5: Counting Bits includes an alternative approach - parallel summing of adjacent bits:
Since number of instructions in this algorithm does not depend on the value of x, its time complexity is constant (O(1)).
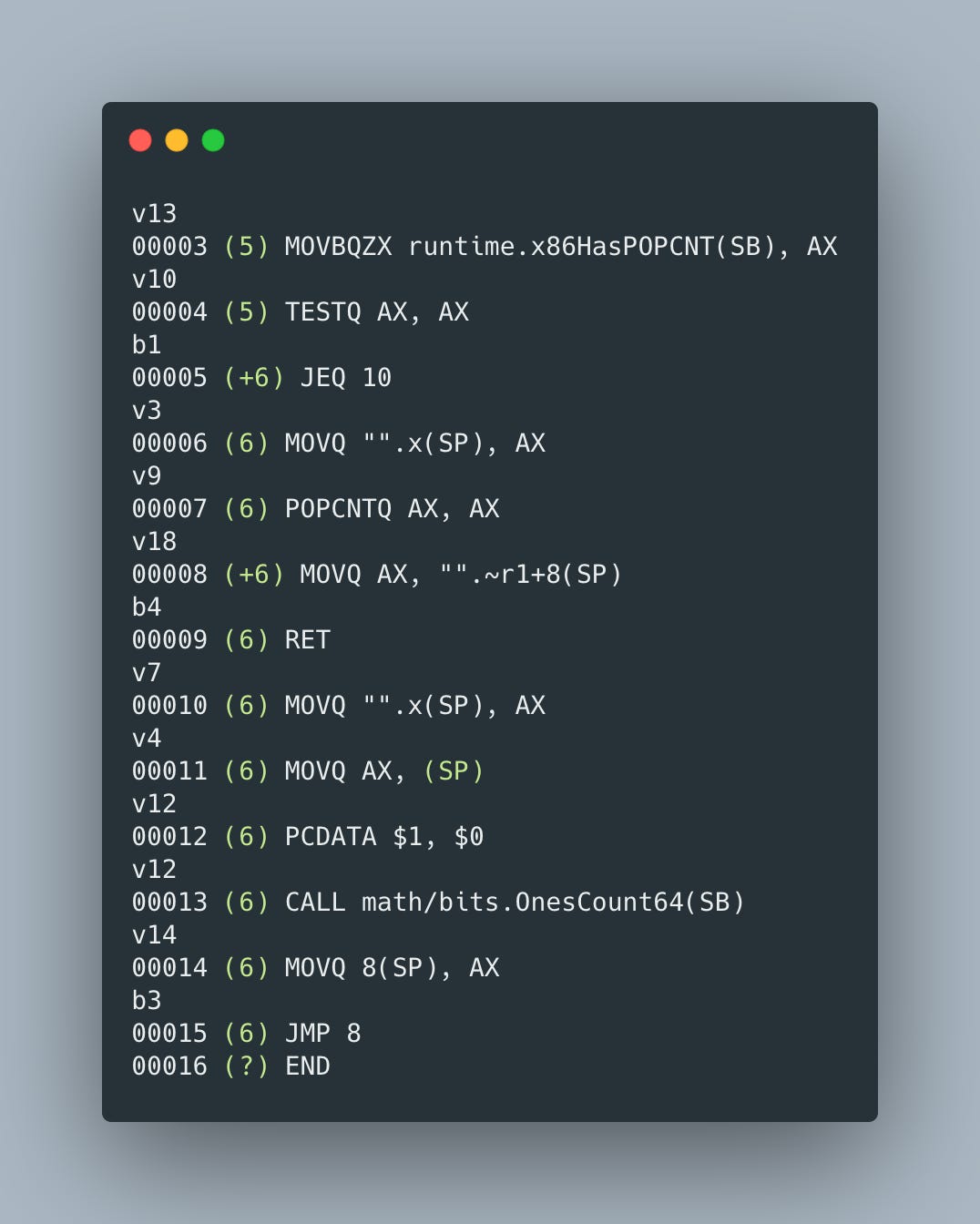
And finally, it’s possible to take advantage of the hardware support, if available, and use POPCNT instruction and that’s exactly what Go’s OnesCount64 function from math/bits package does by translating bits.OnesCount64(x) into
Note that in order to use POPCNT instruction, runtime first has to check if it’s supported by the hardware. This can be established via runtime.x86HasPOPCNT(SB). So the final implementation in our list is going to be
Now that we have all implementations, it’s time to put them to the test and use benchmarks to find out which implementation is the fastest.
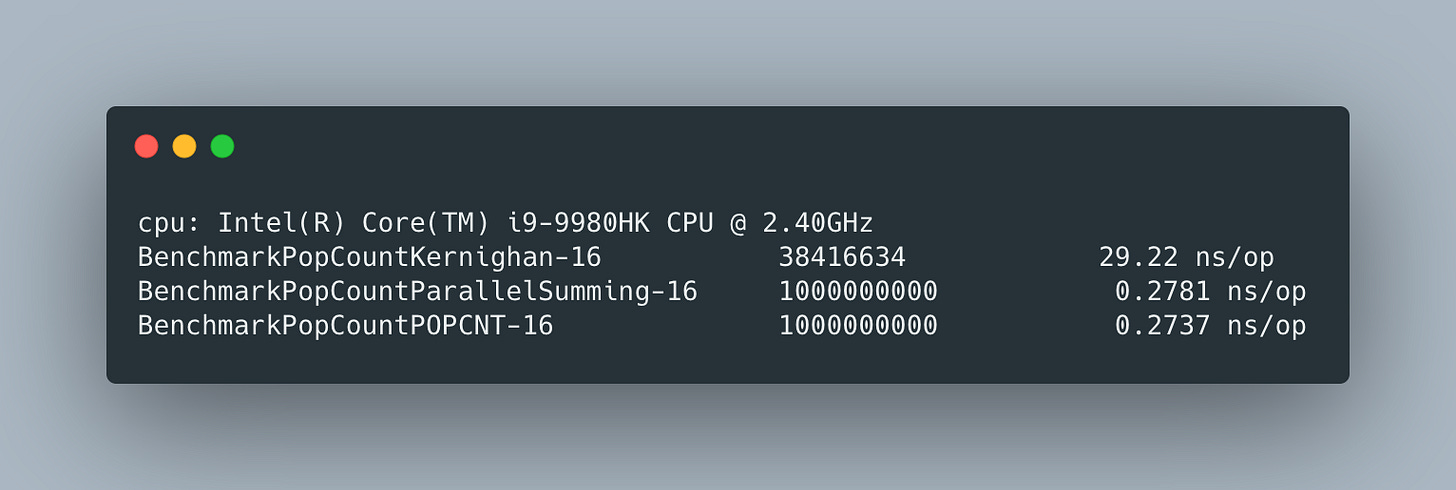
To see how the number of set bits impacts the execution time, we’ll use a constant x. When none of the bits are set, performance of all implementations is fairly close, although Kernighan’s algorithm took ~2X time:
But when we set all the bits, constant time implementations demonstrate significant advantage:
Constant time implementations are more than 100X faster and have very similar performance. Usage of POPCNT instruction would be faster, if not for the extra runtime check, but considering how flexible and easy to use it is, we should always try to take advantage of our hardware.